The circuit of the "exclusive or" has two inputterminals, which are linked. The output is 1 ("true"), if there is an odd number of ones at the inputs. The meaning of the "either .. or" shows it well, "either" there is one inputterminal true "or" the other one. They have to be different for getting an 1 (true) as a result.
claim: Either I or you win.
(The claim is false if both or nobody of them wins.)
| If ... | the claim is ... |
|---|---|
| Nobody wins, | wrong |
| you win, | true |
| I win, | true |
| We both win, | false |
claim (Z) = Either I(A) or you(B) win.
| A | B | Z |
|---|---|---|
| loses | loses | false |
| loses | wins | true |
| wins | loses | true |
| wins | wins | wrong |
Z = I XOR you (wins)
1: victory/ true
0: defeat/ wrong
A XOR B = Z
| A | B | Z |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

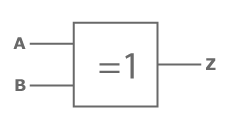
" =1 " (if there is exactly one 1 (with 2 inputterminals), then true)
claim: Either it rains or the sun shines.
If the sun shines AND it's not raining, the claim is _________.
true
If the sun shines and it's raining _________.
wrong
It possible to have an XOR gate with more than two inputterminals the result is calculated in the same way
like a gate with two inputterminal. The result is also true, if there is an odd number of inputterminals with an one. It's implemented with many XOR gates, where two inputterminals are connected with a xor and the
result is (xor) connected with the next input. This process is repeated until every input is considered.
addition of binary numbers in the Von Neumann architecture
| exlusive or | addition | result |
|---|---|---|
| 0 XOR 0 | 0 + 0 | 0 |
| 0 XOR 1 | 0 + 1 | 1 |
| 1 XOR 0 | 1 + 0 | 1 |
| 1 XOR 1 | 1 + 1 | (1)0 |
encryption: One-Time-Pad
(plaintext → binary text XOR random key (same length as binary text)= secret message;
secret message XOR key = binary text → plaintext)
more information
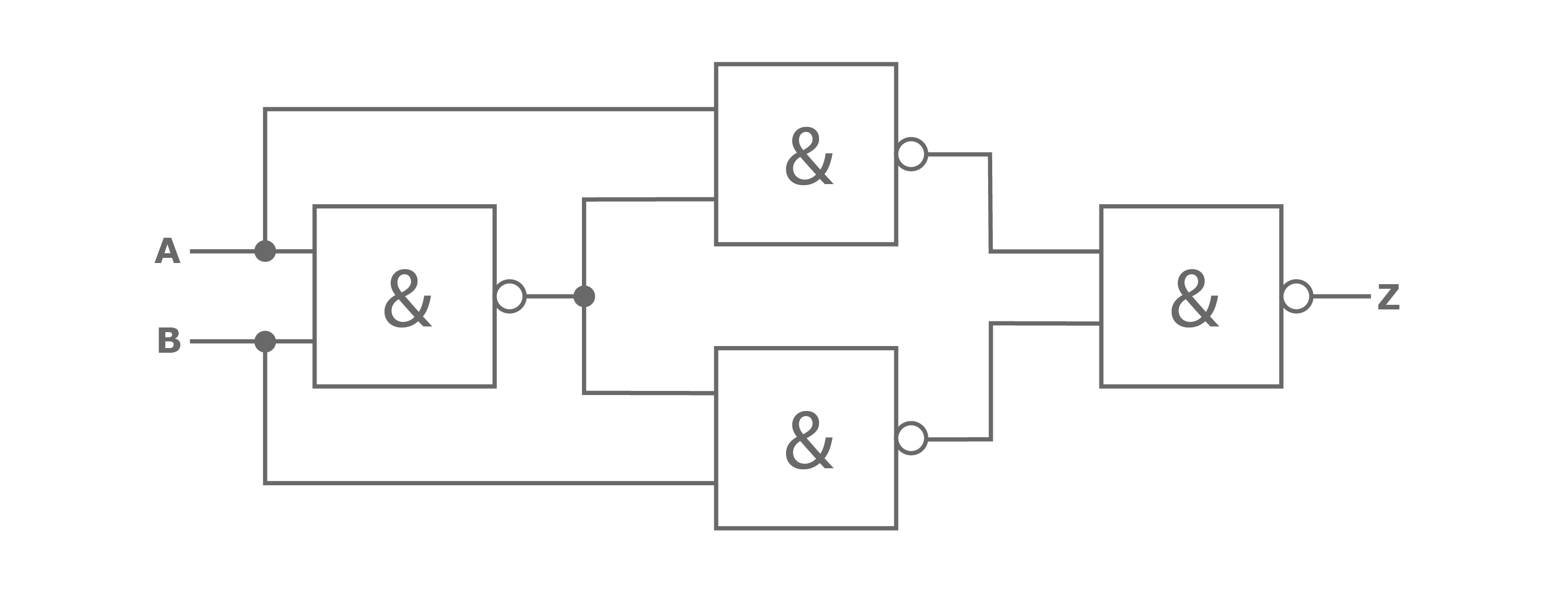
It is also possible to build this gate just from NAND gates.