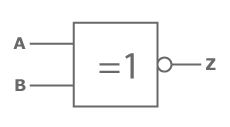
The Equivalence gate checks the input signals and returns "true" in case of equality.
It can be compared with a gamble for two persons in which every person draws one lot. On these lots either the symbol "pear" or "apple" is shown. The two persons play in one team, which wins only under certain combinations of "apple" and "pear". In a gamble of the type equivalence they would only win, if both draw the same lot. Specifically, this means "apple" and "apple" or "pear" and "pear" are the valid combinations.
Claim (Z) = Both persons will draw the same symbols on their lots.
| A | B | Z |
|---|---|---|
| pear | pear | true |
| pear | apple | false |
| apple | pear | false |
| apple | apple | true |
Z = A XNOR B
| A | B | Z |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

Claim: Tom and Maria will achieve an equivalent result at the exam. (we just regard wheter one passes the exam, the grade is irrelevant)
Tom fails at the exam and Maria closely passes her exam. ________.
(false)
Tom passes the exam and Marias result is better then Tom's. _________.
(true)
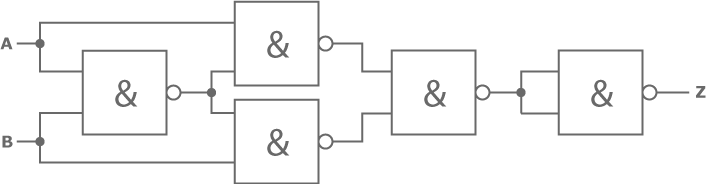
An Equivalence circuit can be built from a XOR circuit and a negator.