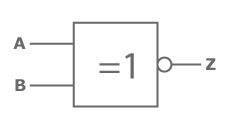
Das Äquivalenz-Gatter prüft die Eingabesignale auf Gleichheit und gibt im Falle dieser ein „wahr“ aus.
Man kann dies mit einem Losspiel vergleichen bei dem zwei Personen Lose ziehen, auf denen entweder das Symbol „Apfel“ oder „Birne“ aufgedruckt ist. Sie spielen als Team und das Team gewinnt nur unter festgelegten Kombinationen aus „Apfel“ und „Birne“. Bei einem Spiel des Typs Äquivalenz würden sie nur gewinnen, wenn sie beide das gleiche Los ziehen würden. Das heißt bei „Birne“ und „Birne“ oder bei „Apfel“ und „Apfel“.
Behauptung (Z) = Beide Personen werden das gleiche Lossymbol ziehen.
| A | B | Z |
|---|---|---|
| Birne | Birne | Wahr |
| Birne | Apfel | Falsch |
| Apfel | Birne | Falsch |
| Apfel | Apfel | Wahr |
Z = A XNOR B
| A | B | Z |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Abb. x.2 Schalttabelle (<Äquivalenz>)

Sprachliche Aussagenlogik:
Behauptung: Tom und Anja werden in der Prüfung ein äquivalentes Ergebnis erzielen (es zählt nur bestanden oder durchgefallen, die Note ist irrelevant)
Tom fällt durch, doch Anja besteht gerade noch so. ________.
(falsch)
Tom besteht die Prüfung und Anjas Ergebnis ist besser als Toms. _________.
(wahr)
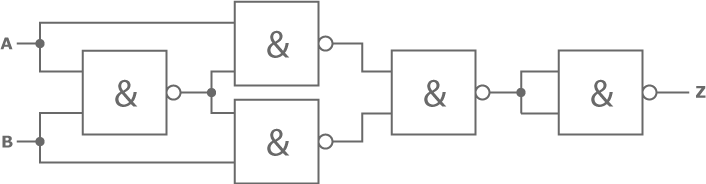
Ein Äquivalenz-Gatter lässt sich durch ein XOR-Gatter mit nachgeschalteter Negation aufbauen.