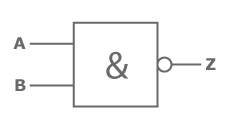
Das NAND-Gatter ist die Negation des AND-Gatters und gibt nur „falsch“ aus, wenn beide Eingangsignale „wahr“ sind. Andernfalls ist die Rückgabe immer „wahr“.
Ich wette darauf, dass Marathonläufer A und Marathonläufer B nicht beide das Ziel erreichen ( = 1), sondern mindestens einer vorher aufgibt ( = 0). Sollten doch beide die gesamte Strecke absolvieren, habe ich verloren. In den anderen Fällen bekomme ich meinen Wettgewinn ausgezahlt.
Behauptung Z = Läufer A und Läufer B erreichen nicht beide das Ziel.
| A | B | Z |
|---|---|---|
| Gibt auf | Gibt auf | Wettgewinn |
| Gibt auf | Schafft es | Wettgewinn |
| Schafft es | Gibt auf | Wettgewinn |
| Schafft es | Schafft es | Wette verloren |
Z = A NAND B
| A | B | Z |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Abb. x.2 Schalttabelle (<NAND>)

Sprachliche Aussagenlogik:
Behauptung: Heute kann es schneien oder regnen, jedoch nicht beides.
Das Wetter bleibt den ganzen Tag heiter. (wahr)
Es schneit. (wahr)
Der anfängliche Regen geht in Schnee über. (falsch)
Das NAND-Gatter ist einer der Grundbausteine der Schaltungslogik. Aus diesem Gatter kann jedes andere Gatter gebaut werden.
So zum Beispiel ein AND:
x AND y = (x NAND y) NAND (x NAND y)